5.4 estimateErrors

Estimating PMD pattern and Sequencing Errors

estimateErrors uses genotype likelihood model to estimate the likelihood of sequencing errors and PMD using Expectation Maximization (EM) algorithm. The sequencing errors are recalibrated based on quality score of reads, fragment length, mapping quality, position in the read and context.

See Additional information for detailed description of the model.

5.4.1 Input

Required inputs :

--bam Input_bam_file.bam	Input bam file.
--fasta Input_refrence_genome_file.fasta	Reference genome.

Optional inputs :

--recalModel recal_model	Semicolon separated recalibration model indicating which covariates and which regression model (empiric or polynomial) to use, e.g."intercept;quality:polynomial3;position:polynomial3;fragmentLength:polynomial3;mappingQuality:polynomial3;context;". Default = all five covariates are used and empiric regression is used for all.
--pmdModel pmd_model	pmd model to be used, e.g."CT5:0.2*exp(-0.3*p)+0.01;GA3:0.5*exp(-0.2*p)+0.01". Default = CT5;GA5;CT3;GA3.

Specific Parameters :

• See Filter parameters to apply specific filters for bases, reads and parsing window setting.

Engine parameters that are common to all tasks can be found here.

5.4.2 Output

5.4.3 Usage Example

#! /bin/bash

. $(dirname $0)/find_atlas

recal="intercept[.0];quality:polynomial[0.95,0.01];position:polynomial[0.02]"
pmd="CT5:0.2*exp(-0.3*p)+0.01;GA3:0.2*exp(-0.3*p)+0.01"

delta=10
k="111"
L="100$k"

. $(dirname $0)/simulate --recal $recal --pmd $pmd  \
    --type "HKY85" --mu 0.55 --thetaG 0.00033 --thetaR 0.015 \
  --chrLength $L,$L --depth 9 --ploidy 2,1 --numReadGroups 3 \
  --baseQuality 'categorical(12:1237,22:845,27:1912,32:21069,37:34246,41:339557)' \
  --fragmentLength 'normal(40,10)[30,101]' \
  --mappingQuality 'normal(60,10)[30,60]' --fixedSeed 80

echo "chr1 0 $L" > bed1.bed
echo "chr2 0 99$k" > bed2.bed

echo "readGroup poolWith" > recal.pool
echo "SimReadGroup2 SimReadGroup1" >> recal.pool

echo "readGroup poolWith" > pmd.pool
echo "SimReadGroup3 SimReadGroup1" >> pmd.pool

out="estimateErrors"
$atlas --task estimateErrors --minDeltaLL $delta \
       --bam simulate.bam --fasta simulate.fasta \
       --poolRecal "all" --poolPMD "all" \
       --fixedSeed 81 --out $out --logFile $out.out 2> $out.eout

recalModel="intercept;quality;position:polynomial1;fragmentLength:polynomial2;mappingQuality;context"
out="specificModel"
$atlas --task estimateErrors --minDeltaLL $delta --recalModel $recalModel \
       --bam simulate.bam --fasta simulate.fasta \
       --regions bed1.bed,bed2.bed --ploidy 2,1 --window 45672 --writeRestart \
       --poolRecal "recal.pool" --poolPMD "pmd.pool" \
       --fixedSeed 82 --out $out --logFile $out.out 2> $out.eout

Additional Information

Genotype likelihood model for PMD and sequencing error recalibration

The model implemented in ATLAS estimates three parameters in parallel, namely genotype distribution, PMD and recalibration parameter which is described below.

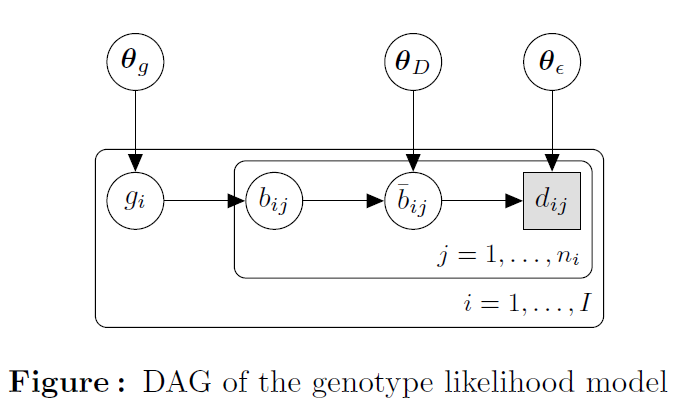
The figure above shows the directed acyclic graph (DAG) of the model, where the hidden genotype at site \(i = 1, . . . , I\) are given by \(g_{i}\), where \(g_{i} = AA,AC, . . . , TT\) is one of the 10 possible diploid genotypes; the sequencing data of a single individual at site \(i\) consist of \(n_{i}\) reads that cover this site and the base of read \(j\) covering site \(i\) is denoted by \(d_{ij} = A,C, G, T, j = 1, . . . , n_{i}\).

The data \(d_{ij}\) observed at a site \(i\) with true genotype \(g_{i}\) is a function of four processes:

• The distribution of genotypes \(g_{i}\) within the genome, and let \(\theta_{g}\) denote the parameters governing that distribution.

• The random sampling of alleles of from genotypes. We will denote by \(b_{ij} = A,C, G, T\) the sampled allele in read \(j\) covering site \(i\). Given a genotype \(g_{i} = k l\) with \(k, l = A,C, G, T\) at that site we have

\[P(\boldsymbol{b_{ij}}|g_{i} = k,l) = \frac{1}{2}[Ind(b_{ij}=k) + Ind(b_{ij}=l)] = \begin{cases} 1 & \text{if } b_{ij}=k=l,\\ \frac{1}{2} & \text{if } k \neq l \text{ and } b_{ij}=k \text{ or } b_{ij }=l,\\ 0 & \text{otherwise. } \end{cases}\]

The subset of bases that make up genotype \(g\) are denoted by \(b ∈ g\).

• PMD that potentially modifies \(b_{ij}\). We will denote the resulting base by \(\bar{b}_{ij} = A,C, G, T\) and by \(\theta_{D}\) the parameters governing PMD. In the case of no PMD, \(b=\bar{b}\).

• Sequencing errors may result in \(d_{ij} \neq \bar{b}_{ij}\). The parameters governing sequencing errors is denoted by \(\theta_{ϵ}\).

Assuming independence among sequencing reads when conditioned on \(g_{i}\), we then have,

\[\mathcal{L}(\boldsymbol{\theta_{g},\theta_{D},\theta_{ϵ}}) = P({d}|\theta_{g},\theta_{D},\theta_{ϵ}) = \prod_{i=1}^{I}\sum_{g}P({g}|\theta_{g})\prod_{j=1}^{n_{i}} [\sum_{bϵg}P(b|g)\sum_{\bar{b}|b}P(\bar{b}|b,\theta_{D})P(d_{ij}|\bar{b},\theta_{ϵ})], \] where \(d = (d_{1}, . . . , d_{I})\) denotes the full data with \(d_{i} = (d_{i1}, . . . , d_{ini})\).

This formulation is very general and allows for different models regarding the distribution of genotypes \(P(g|\theta_{g})\), PMD \(P(\bar{b}|b,\theta_{D})\) and sequencing errors \(P(d_{ij}|\bar{b},\theta_{ϵ})\).

Implemented models regarding sequencing errors

During implementation of the model regarding sequencing errors i.e. the probability function \(P(d_{ij}|\bar{b},\theta_{ϵ})\), ATLAS assumes that,

\[P(d_{ij}|\bar{b},\theta_{ϵ}) =P(d_{ij}|\bar{b},\rho,\master) = \begin{cases} 1 - ϵ(q_{ij},\master) & \text{if } d_{ij}=\bar{b},\\ ϵ(q_{ij},\master)\rho_{\bar{b}d_{ij}} & \text{if } d_{ij} \neq \bar{b}, \end{cases}\]

where \(ϵ(q_{ij},\master)\) is the relevant sequencing error rate and \(\rho_{kl}\) reflects the relative rate for a sequencing error at a particular base \(k = A,C, G, T\) to result in any of the three alternative bases \(l \neq k\).

\[0 \leq \rho_{kl} \leq 1, \sum_{l\neq k} \rho_{kl}= 1 \quad\quad k,l =A,C,G,T \]

The error rates \(ϵ(q_{ij},\master)\) themselves are functions of a given external vector of information $q_{ij} with parameters \(θ_{ϵ}. ATLAS then, assumes the logistic model\)$ ϵ_{ij} = ϵ(q_{ij},) = {0}+ {l=k}^{K} {k}(q{ijk},_{k}) $$

with \(K\) covariates $q_{ij} = {q_{ij1}, . . . . . . , q_{ijK} of which each has a function \(\psi_{k}(q_{ijk},\master_{k})\) with parameters \(\master k\). Thus the total parameter vector is $ {ϵ} = (,)$ with $ = ({AC},{AG}, . . . . . ,{TG})$ and \(\master = \{\master_0, . . . . . , \master_K\}\).

• The parameters \(\theta_{ϵ} = (\rho,\master)\) is estimated using the general EM algorithm introduced above.

ATLAS considers the following potential covariates:

• The transformed machine-reported quality score \(\tilde{Q}_{ij}\) . We transform the original quality score \({Q}_{ij}\) as

\[\tilde{Q}_{ij} =log(\frac{e_{ij}}{1-e_{ij}}); e_{ij}=10^{-Q_{ij}/10} \] to ensure that using \(\eta_{ik}(\master) = \tilde{Q}_{ij}\) results in no transformation.

• The position within the read \(p_{ij}\), either as with parameter \(\master_{p}\).

• The sequencing context \(c_{ij}\) , i.e. the base that was reported just previously of the current base \(d_{ij}\) in 5’–>3’ direction (i.e. \(c_{ij} = d_{ij-1}\) for forward mapping reads and(i.e. \(c_{ij} = d_{ij+1}\) for reverse mapping reads).

Importantly, we will also infer an independent error model (i.e. independent \(\master\)) for each read group.

Implemented models regarding PMD

A characteristic feature of ancient DNA is post-mortem damage (PMD). The most common form of PMD is C-deamination, which leads to a C → T transition on the affected strand and a G → A transition on the complimentary strand. These deaminations do not occur randomly along the whole read, but instead are observed much more frequently at the beginning of a read. This is due to fragment ends being more often single-stranded and thus subject to a much higher rate of deamination.

During implementation of the model regarding PMD i.e. the probability function \(P(\bar{b}|b,d_{ij})\), In case of C → T damage,

\[P(\bar{b}|b,d_{ij}) = \begin{cases} 1 & \text{if } \bar{b} = b \text{ and } b \neq C\\ 0 & \text{if } \bar{b} \neq b \text{ and } b \neq C\\ D_{ij} & \text{if } \bar{b} = T \text{ and } b = C\\ 1 - D_{ij} & \text{if } \bar{b} = C \text{ and } b = C , \end{cases}\]

where \(D_{ij}\) denotes the probability that the base \(j\) at site \(i\) was affected by PMD. Analogously, in case of G → A damage,

\[P(\bar{b}|b,d_{ij}) = \begin{cases} 1 & \text{if } \bar{b} = b \text{ and } b \neq G\\ 0 & \text{if } \bar{b} \neq b \text{ and } b \neq G\\ D_{ij} & \text{if } \bar{b} = A \text{ and } b = G\\ 1 - D_{ij} & \text{if } \bar{b} = G \text{ and } b = G , \end{cases}\]

ATLAS assumes that the rate $D_{ij} = D(q_{ij} , θ_{D}) as well as the type of PMD damage to occur to be a function of a given external vector of information \(q_{ij}\). Specifically, it models \(D_{ij}\) as a function of the distance \(\delta_{ij}\) in bases from the nearest end \(e_{ij} ∈ {5′, 3′}\) of the fragment (in case of paired-end sequencing) or read (in case of single end sequencing).

Let \(\psi = (\psi_{1}, . . . , \psi_{M})\) be the vector of PMD probabilities for distances \(m = 1, . . . ,M\) up to a maximum distance \(M\). We then have,

\[D_{ij} = f(\delta_{ij}) = \begin{cases} \psi_{M} & \text{if } \delta_{ij} \geq M\\ \psi_{\delta_{ij}} & \text{otherwise }, \end{cases}\]

ATLAS considers the following additional categorical information:

• It fits independent patterns for each read group.

• It uses different PMD patterns depending on whether a single-strand or double strand sequencing library was prepared:

  • For single-strand libraries, ATLAS assumes that for forward mapping reads C → T damage occurs on both ends while for reverse mapping reads G → A damage occurs at both ends. It further assumes that damages occur at the same rates (i.e. at the same \(\psi\)) for both types of reads at both ends.
  • For double-strand libraries, ATLAS assumes that for forward mapping reads C → T damage occurs at 5’ ends and G → A damage at 3’ ends, and the inverse for reverse mapping reads. It further assumes that damages occur at the same rates at 5’ ends of both forward and reverse mapping reads, and, equivalently, at the same rates at 3’ ends of both types of reads.

• ATLAS distinguishes between single-end and paired-end sequencing:

  • For single-end sequencing, the 5’ end of the read always marks the 5’ end of the fragment, and the distance \(δ_{ij}\) measured from it thus reflects the distance relevant for PMD. ATLAS will thus infer a common pattern for all single-end read lengths at the 5’ end. The sequencing read may not reach the 3’ end of the fragment, however. Among the reads with lengths matching the maximum number of sequencing cycles \(C_{max}\), for which \(δ_{ij}\) measured from the 3’ end underestimates the true distance to the 3’ end of the fragment. This leads to a reduced PMD rate compared to the 5’ end at the same distance \(δ_{ij}\) . Due to errors during adapter removal, this issue may also affect reads a few bases shorter than \(C_{max}\). ATLAS will thus infer a common pattern for all reads shorter than \(C_{max} − S\) and a different pattern for all reads of each of the lengths $ C_{max},C_{max} − 1, . . . ,C_{max} − S$, where \(S\) is a user-defined threshold (typically 5 bases).
  • For paired-end sequencing, both ends are known and the distances \(δ_{ij}\) properly reflect the distance to those ends. ATLAS thus uses a single PMD pattern for all fragment lengths.